Background Extraction

The sky background often has an unwanted gradient caused by light pollution, the moon, or simply the orientation of the camera relative to the ground. This function samples the background at many places of the image and looks for a trend in the variations and removes it following a smoothed function to avoid removing nebulae with it.

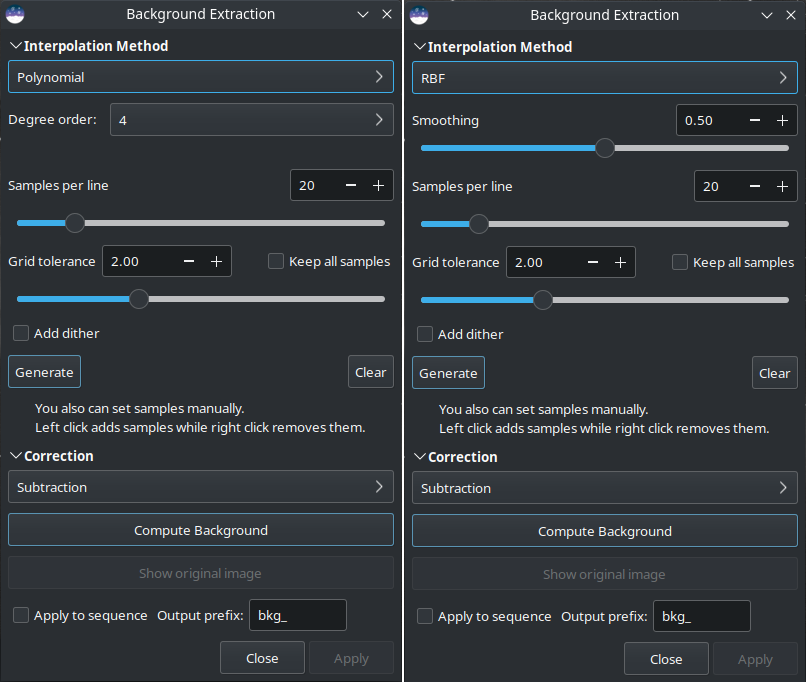
Background extraction dialog box. On the left is the polynomial version, on the right RBF.

Samples can be automatically placed by providing a density (Samples per line) and clicking on Generate. If areas of the image are brighter than the median by some factor Grid tolerance times sigma, then no sample will be placed there.

There are some options regarding how to place samples.

• The default is a regular grid, however you can select random sample locations to achieve the same sample positioning as SetiAstro's AutoDBE process.

• You can select sample optimization. If this is enabled, the position of each sample will be optimized by seeking a local minimum sample median. This may result in an irregular grid. Note that this setting also affects manually placed samples, so don't be surprised if your samples move! If you wish to place a sample precisely then disable this.

You can also limit the area in which samples are placed. If a sample lands too close to the image edge it may include black border areas, or areas of uneven coverage, resulting in a poor background model. By making a selection a little in from the image edge, you can restrict the sample placement to inside the selection thus eliminating the problem with edge samples.

Tip

If you have very strong gradients, for example when imaging in high Bortle urban skies, even the maximum grid tolerance may be insufficient. In this case you can check the Keep all samples checkbox and the full sample grid will be populated. You will then need to remove samples from actual astronomical objects manually.

After generation, samples can also be added manually (left click) or removed manually (right click).

There are two algorithms to remove the gradient:

RBF

This is the most modern method. It uses the radial basis function to synthesize a sky background to remove the gradient with great flexibility. It requires a single parameter which is present in the form of a slider: Smoothing. With this value you can determine how soft or hard the transition between the sample points is calculated. A high smoothing factor makes sense for large and uniform gradients, and a correspondingly lower value for small, local gradations.

Tip

Start with the basic setting (50%) and gradually tweak for optimal results.

Theory

Radial basis functions are functions of the form \(\phi(\mathbf{x}) = \phi(\| \mathbf{x} \|)\), whereby in our case we use the Euclidean norm \(\| \mathbf{x} \| = \sqrt{x_1^2 + x_2^2}\). The function \(f\), which describes the background model, can now be expressed as a linear combination

\[f(\mathbf{x}) = \sum_i w_i \, \phi(\|\mathbf{x} - \mathbf{x_i}\|) + o\]

where \(w_i\) corresponds to the weights for the different sample points and \(o\) corresponds to a constant offset.

The requirement that the function \(f\) should pass through the sample points results in the condition

\[\begin{split}\begin{pmatrix} \phi(\mathbf{x}_1 - \mathbf{x}_1) & \phi(\mathbf{x}_1 - \mathbf{x}_2) & \dots & \phi(\mathbf{x}_1 - \mathbf{x}_N) & 1 \\ \phi(\mathbf{x}_2 - \mathbf{x}_1) & \phi(\mathbf{x}_2 - \mathbf{x}_2) & \dots & \phi(\mathbf{x}_2 - \mathbf{x}_N) & 1 \\ \vdots & \vdots & \ddots & \vdots \\ \phi(\mathbf{x}_N - \mathbf{x}_1) & \phi(\mathbf{x}_N - \mathbf{x}_2) & \dots & \phi(\mathbf{x}_N - \mathbf{x}_N) & 1 \\ 1 & 1 & \dots & 1 & 0 \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_N \\ o \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \\ 0 \end{pmatrix} \, ,\end{split}\]

which can only be fulfilled if the matrix on the left-hand side is invertible. With the right choice of function \(\phi\) this can always be guaranteed [Wright2003].

In addition, the summand \(s \, I\) is added to the matrix on the left-hand side, where \(s\) is a smoothing parameter and \(I\) is the unit matrix. The summand causes a regularization, which results in a smoother result the larger the parameter \(s\) is. This parameter can be changed with the Smoothing parameter of the dialog box.

For the radial basis function, we use the thin-plate spline \(\phi(|\mathbf{x}|) = |\mathbf{x}|^2 \log(|\mathbf{x}|)\).

Polynomial

This is the original and simplest algorithm developed in Siril. Only one parameter is used in polynomial computation: the Degree order. The higher the degree, the more flexible the correction, but a too high degree can give strange results like overcorrection.

Tip

A degree 1 correction can be very useful for when you want to remove the gradient on the subs.

Warning

Background removal can be carried out on CFA images, but only if they have Bayer patterns. (It is not supported for X-TRANS patterns.) For Bayer patterned images, the image is treated as four spatially interleaved images, each corresponding to a CFA subchannel. Each subchannel is independently processed to remove its gradient and then the subchannels are recombined into the original interleaved pattern.

The intended use for this is to remove linear gradients from sequence frames prior to using Drizzle on a Bayer patterned sequence, and in that case it is strongly recommended to use linear (polynomial order 1) gradient removal as with other pre-stacking gradient removal.

Theory

Polynomial functions are functions of the form

\[\begin{equation} f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_2x^2+a_1x+a_0 \end{equation}.\]

In Siril, the maximum degree allowed is \(n=4\) and can be modified using the Degree order drop-down menu. Beyond this, the model is generally unstable and gives poor results.

General settings

• Add dither: Hit this option when color banding is produced after background extraction. Dither is an intentionally applied form of noise used to randomize quantization error, preventing large-scale patterns such as color banding in images.

• Correction:

  • Subtraction: it is mainly used to correct additive effects, such as gradients caused by light pollution or by the Moon.

  • Division: it is mainly used to correct multiplicative phenomena, such as vignetting or differential atmospheric absorption for example. However, this kind of operation should be done by master-flat correction.

• Compute Background: This will compute the synthetic background and will apply the selected correction. The model is always computed from the original image kept in memory allowing the user to work iteratively.

• Show original image: Keep pressing this button to see the original image.

The background gradient of pre-processed image can be complex because the gradient may have rotated with the acquisition session. It can be difficult to completely remove it, because it’s difficult to represent it with a polynomial function. If this is the case, you may consider removing the gradient in the subexposures: in a single image, the background gradient is much simpler and generally follows a simple linear (degree 1) function.

Tip

Sometimes unsightly color banding appears after background extraction. When this happens, there are two things to check. Firstly, if the image is in 16-bit, we strongly advise you to always use the 32-bit format. If, despite everything, you still observe such artifacts, the add dither option, explained above, is the solution to your problem.

When such banding occurs after gradient extraction. It can be solved with the add dither option (Courtesy of Nathan B.).

Tip

Good results with the RBF algorithm generally require fewer samples than with the polynomial algorithm.

See also

For more explanations, see the corresponding tutorial here.

Siril command line

subsky { -rbf | degree } [-dither] [-samples=20] [-tolerance=1.0] [-smooth=0.5] [-existing]

Computes a synthetic background gradient using either the polynomial function model of degree degrees or the RBF model (if -rbf is provided instead) and subtracts it from the image.

The number of samples per horizontal line and the tolerance to exclude brighter areas can be adjusted with the optional arguments. Tolerance is in MAD units: median + tolerance * mad.

Dithering, required for low dynamic gradients, can be enabled with -dither.

For RBF, the additional smoothing parameter is also available. To use pre-existing background samples (e.g. if you have set background samples using a Python script) the -existing argument must be used

Tip

The -existing command argument forces use of existing background samples. This option is primarily for use in conjunction with the Python module where SirilInterface.set_bgsamples() can be used to set custom background samples based on user-defined algorithms. If it is not provided, subsky will automatically regenerate background samples. Note that the -existing option is not available with the seqsubsky command, because sequence frames are not necessarly registered at the time background subtraction is carried out, so the samples for one frame do not necessarily apply to another.

Siril command line

seqsubsky sequencename { -rbf | degree } [-nodither] [-samples=20] [-tolerance=1.0] [-smooth=0.5] [-prefix=]

Same command as SUBSKY but for the sequence sequencename.

Dithering, required for low dynamic gradients, can be disabled with -nodither. Note that the -existing option is not available for sequence background removal, as the frames of a sequence are not necessarily always aligned.

The output sequence name starts with the prefix "bkg_" unless otherwise specified with -prefix= option. Only selected images in the sequence are processed

Links: subsky

[Wright2003]

Wright, Grady Barrett. Radial basis function interpolation: numerical and analytical developments. University of Colorado at Boulder, 2003.