Noise Reduction
Image Noise
Images suffer from various types of noise:
Impulse noise
This type of noise (sometimes called “salt and pepper noise”) typically arises from hot or cold pixels. It is usually dealt with by using sigma rejection stacking, but sometimes you may need to deal with it if processing a single unstacked image.
Additive White Gaussian Noise
This type of noise is typical of well-illuminated photographs: it arises from the thermal and electronic fluctuations of the acquisition device, and the noise level is independent of the signal. AWGN can be reduced at capture time by using cooled cameras, and it is reduced in stacking because stacking \(n\) images increases the correlated signal by a factor of \(n\) whereas the uncorrelated noise only increases by a factor of \(\sqrt{n}\). It is also the type of noise that most classical denoising algorithms are designed to remove.
Poisson Noise
When dealing with photon-starved images, the character of the noise ceases to be primarily Gaussian and the probabilistic nature of photon counting becomes significant or even dominant. This is modelled by a Poisson distribution and this type of noise is signal dependent.
Noise Reduction in Siril
Siril provides well-studied state-of-the-art classical denoising algorithms. The criteria for choosing algorithms were:
The algorithm should be analysed in peer reviewed academic journals, with a description of the algorithm and an objective quantitative comparison of its performance.
The authors should have made available a F/OSS implementation. This is important to avoid IP issues and, where the reference implementations have been used directly, to ensure licence compatibility.
The algorithms should perform at a reasonable speed.
Finally, the implementation of the algorithm must be capable of processing 32 bit floating point pixel data.
Neural network denoising technology was investigated, but discounted at the current time on the grounds of development complexity. The denoising performance of neural networks can typically beat classical approaches by up to a dB peak signal-to-noise ratio, but performance is highly dependent on the neural network being trained on data representative of the real live data.

Noise Reduction dialog
Algorithms: Impulse Noise
Siril primarily removes impulse noise through sigma rejection stacking. If you use this stacking method, you shouldn’t have any issues with impulse noise. However if you are working on a single exposure you may well find impulse noise in your image. This should be dealt with using Siril’s Cosmetic Correction function before any other noise reduction is used, as the presence of impulse noise can skew AWGN denoising algorithms and create artefacts. It works in a similar way to sigma rejection, but on neighbouring pixels. Any pixel whose intensity is more than n standard deviations away from its neighbours will be rejected and replaced by a value based on the median of the neighbours. In the Denoising tool Cosmetic Correction is active by default and will take place before any additional denoising steps. (Even if impulse noise removal has already been carried out, leaving the setting on does no harm.) Alternatively, Cosmetic correction can be applied manually using the Cosmetic Correction tool in the Image Processing menu.
Algorithms: Additive White Gaussian Noise
The main AWGN noise reduction algorithm used in Siril is Non-Local Bayesian (NL-Bayes) denoising [Lebrun2013].
Non-local denoising algorithms represented a major improvement over previous pixel-centred linear filters. NL-Bayes is an improved version of the earlier non-local denoising algorithms and offers one of the best classical AWGN denoising algorithms. It is marginally better than the modern “benchmark” algorithm Block Matching and 3D tranform (BM3D) noise reduction and much faster to execute.
The key parameter required to optimise the performance of AWGN algorithms is sigma, the standard deviation of the noise. Siril measures the noise level directly from the image data and passes this to the NL-Bayes algorithm, therefore in the Siril denoising tool there are no configurable inputs to NL-Bayes.
Siril complements NL-Bayes with a number of other noise reduction algorithms:
Data-Adaptive Dual Domain Denoising (DA3D) [Pierazzo2017]
This takes the output of NL-Bayes and uses it as a guide image. This guide image is used to reprocess the original image by performing frequency domain shrinkage on shape and data-adaptive patches. It slightly improves the performance of NL-Bayes at some additional computational cost. The shape and data-adaptive patches are dynamically selected, thus concentrating the computations on the areas with greatest image detail. It can also help to reduce staircase artefacts present in the guide image.
In the Siril denoising tool, DA3D is a simple toggle with no optional settings.
Strengthen, Operate, Subtract iteration (SOS) [Romano2015]
SOS works by iterating the primary denoising algorithm several times. At each iteration the image is "strengthened" by mixing in a proportion of the original noisy image. The NL-Bayes algorithm runs on this strengthened image, after which the previous estimation is subtracted.
The image x at an iteration \(k+1\) is given by \(x_{k+1}=f(y+x_k)-x_k\) where \(y\) is the noisy input image.
In the Siril denoising tool, SOS is a toggle with two parameters: the number of
iterationscan be set, and the proportion of the noisy image mixed in at each iteration (rho) can be set. Avoid settingrhotoo high as it can result in issues with SOS converging: the default values (3 iterationsandrho = 0.2) are usually fine.
Algorithms: Poisson and Poisson-Gaussian Noise
Anscombe Variance-Stabilising Transform [Mäkitalo2011], [Mäkitalo2012]
Variance stabilising transforms are used for images with Poisson or Poisson-Gaussian noise to minimise the signal dependence of the noise and make it look more like AWGN, which NL-Bayes is good at removing, and then an inverse transform is applied on completion. The transform chosen for use in Siril is the Anscombe transform \(A: x\rightarrow 2\times \sqrt{\left(x+\frac{3}{8}\right)}\)
As the transform is non-linear, use of the direct algebraic inverse results would bias the output. Siril therefore uses a closed-form approximation to the exact unbiased inverse, which is quick to calculate and produces a substantial improvement over other forms of inverse such as the asymptotic inverse.
In the Siril denoising tool, the Anscombe VST is a simple toggle with no optional settings.
Note that only one of the above mentioned complementary denoising algorithms can be chosen.
The animation below shows what is possible using variance stabilisation with a photon-starved image, in this case a single 5 minute red filter sub of the Pelican nebula, shown with the AutoStretch screen transfer function. Note the lack of blurring, bloating or loss of detail around stars and the sharp edge of the nebula in the bottom left part of the image compared with what might be obtained through more basic noise reduction schemes. Once stretched more sympathetically and combined with other channels this would greatly improve the quality achievable from very limited data (though more data is always the better solution!)

Denoising a photon-starved image
Modulation
In Siril, modulation is a parameter between 0 and 1 mixing the original and denoised images. A value of 1 keeps only the denoised image, a value of 0 does not apply any denoising at all. Modulation obviously reduces denoising performance, but in some instances if denoising has left flat areas of the image looking a little too smooth, you can use some modulation to restore the appearance of microtexture in these regions.
When to run Noise Reduction
The noise reduction algorithms are designed to remove AWGN and should therefore perform best on unstretched images: if white noise has a non-linear stretch applied, its characteristics change and it is no longer white. Performing noise reduction on stretched images can still be done and will result in an improvement, but potentially will not be as effective as if applied at the linear stage.
Noise Reduction Interface
The Siril Noise Reduction tool can be accessed in two ways: via the GUI, or via the command interface. The GUI is shown below. Note: the SOS advanced options are hidden if SOS is not selected.
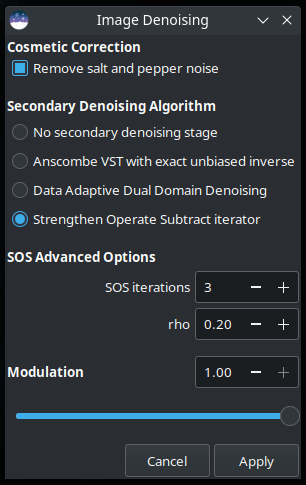
Siril Noise Reduction GUI
Noise reduction can also be applied using Siril commands, either in the console or in scripts. The format is:
Siril command line
denoise [-nocosmetic] [-mod=m] [ -vst | -da3d | -sos=n [-rho=r] ] [-indep]
Comparison
The images below provide a simplistic comparison of the different algorithms. Note that only one image is used: in practice, different algorithms will be better suited for use on different images. All the images can be clicked on to view at 100% zoom.
Original noisy image

Noisy image
Denoised with NL-Bayes only

Denoised with NL-Bayes only
Denoised with NL-Bayes only, with 75% modulation to restore some microtexture

Use of modulation
Denoised with NL-Bayes using the Anscombe transform

Denoised with NL-Bayes, variance stabilised with Anscombe transform. A 200% uninterpolated zoom is shown to the right.
Denoised with DA3D using a NL-Bayes guide image

Denoised with DA3D, guide image prepared using NL-Bayes. A 200% uninterpolated zoom is shown to the right.
Denoised with NL-Bayes and SOS

Denoised with NL-Bayes and SOS iterations. A 200% uninterpolated zoom is shown to the right.
Limitations
The main limitation is that the algorithms work best when the noise is Gaussian in character (or can be made approximately Gaussian using the VST). There are some reasons why this might not be true:
If the image has already been heavily processed, for example with deconvolution or wavelet sharpening, the character of the noise will not generally be Gaussian any more. If both noise reduction and deconvolution form part of your workflow, noise reduction should be done first.
OSC images may denoise less well than mono or composited colour images. A small reduction of luminance AWGN is achieved but as a result of the deBayering process the character of the noise is changed so that it is no longer well modelled as AWGN, and is not removed very effectively. Additionally, for both OSC and composited mono colour images, chrominance noise tends not to be well modelled as AWGN and requires different treatment. At present chrominance noise is best tackled in general purpose image manipulation software such as The GIMP.
References
Lebrun, M., Buades, A., & Morel, J. M. (2013) Implementation of the “Non-Local Bayes” (NL-Bayes) Image Denoising Algorithm. Image Processing On Line, 3 , pp. 1–42. https://doi.org/10.5201/ipol.2013.16
Pierazzo, N., & Facciolo, G. (2017). Data adaptive dual domain denoising: a method to boost state of the art denoising algorithms. Image Processing On Line, 7, 93-114. https://doi.org/10.5201/ipol.2017.203
Mäkitalo, M., & Foi, A. (2012, March). Poisson-gaussian denoising using the exact unbiased inverse of the generalized anscombe transformation. In 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 1081-1084). IEEE. https://doi.org/10.1109/ICASSP.2012.6288074
Makitalo, M., & Foi, A. (2011). A closed-form approximation of the exact unbiased inverse of the Anscombe variance-stabilizing transformation. IEEE transactions on image processing, 20(9), 2697-2698. https://doi.org/10.1109/TIP.2011.2121085
Romano, Y., & Elad, M. (2015). Boosting of image denoising algorithms. SIAM Journal on Imaging Sciences, 8(2), 1187-1219. https://doi.org/10.1137/140990978