Stacking
The final preprocessing step to do with Siril is to stack the images. Image stacking is a technique used in astrophotography to increase the quality and detail of an image by combining multiple photographs into a single, composite image. The process involves taking multiple images of the same object and then align and average the frames together to reduce the noise and increase the signal-to-noise ratio. This results in a final image that has less noise, greater detail and greater dynamic range than a single exposure.
Stacking methods
Sum stacking
This is the simplest algorithm: each pixel in the stack is summed. The increase in signal-to-noise ratio (SNR) is proportional to \(\sqrt{N}\), where \(N\) is the number of images. Because of the lack of normalisation and rejection, this method should only be used for planetary processing.
For 8 or 16 bit per channel input images, the sum is done in a 64 bit integer before being normalized to the maximum pixel value and saved as a 16 bit unsigned integer or 32 bit floating point image.
This stacking method should be used for 8-bit input images because it will increase the dynamic of the images while stacking them, making features discernable. Stacking with an mean or median method such a sequence would only decrease the noise but not improve the dynamic of the image, the result would still be 8 bits deep.
Average Stacking With Rejection
This method of stacking computes a mean of the pixels in a stack after having excluded deviant pixels and an optional normalisation of the images against the reference image. As for sum stacking, the improvement in SNR is proportional to \(\sqrt{N}\). There are several ways to normalize the images and several ways to detect and replace or exclude deviant pixels, explained below.
Warning
Some operating systems limit the number of images that can be opened at the same time, which is required for median or mean stacking methods. For Windows, the limit is 2048 images. If you have a lot of images, you should use another type of sequence, described here.
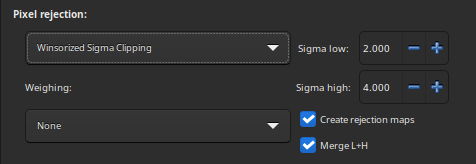
Rejection methods
Percentile Clipping: This is a one step rejection algorithm ideal for small sets of data (up to 6 images).
Sigma Clipping: This is an iterative algorithm which will reject pixels whose distance from median will be farthest than two given values in sigma units(\(\sigma\) low, \(\sigma\) high).
MAD Clipping: This is an iterative algorithm working as Sigma Clipping except that the estimator used is the Median Absolute Deviation (MAD). This is generally used for noisy infrared image processing.
Median Sigma Clipping: This is the same algorithm as Sigma Clipping except than the rejected pixels are replaced by the median value of the stack.
Winsorized Sigma Clipping: This is very similar to Sigma Clipping method, except it is supposed to be more robust for outliers detection, see Huber's work [Peter2009].
Generalized Extreme Studentized Deviate Test [Rosner1983]: This is a generalization of Grubbs Test that is used to detect one or more outliers in a univariate data set that follows an approximately normal distribution. This algorithm shows excellent performances with large dataset of more 50 images.
Linear Fit Clipping [ConejeroPI]: It fits the best straight line (\(y=ax+b\)) of the pixel stack and rejects outliers. This algorithm performs very well with large stacks and images containing sky gradients with differing spatial distributions and orientations.
Rejection maps
The option Create rejection maps computes and creates rejection maps during stacking. These are images showing how many images were rejected for each pixel of the result image, divided by the number of stacked images. If Merge L+H is checked, Siril creates only one rejection map that will be the sum of the low and high maps.

Example of a rejection map (L+H). We can very clearly see the trace of a satellite that has been removed.
Images filtering/weighting
The weighting allows to put a statistical weight on each image. In this way, the images considered to be the best will contribute more than those considered to be the worst. Four methods of weighting are available:
Number of stars weights individual frames based on number of stars computed during registration step.
Weighted FWHM weights individual frames based on wFWHM computed during registration step. This is a FWHM weighted by the number of stars in the image. For the same FWHM measurement, an image with more stars will have a better wFWHM than an image with fewer stars.
Noise weights individual frames based on background noise values.
Number of images weights individual frames based on their integration time.
Median stacking
This method is mostly used for dark/flat/bias stacking. The median value of the pixels in the stack is computed for each pixel.
The increase in SNR is proportional to \(0.8\sqrt{N}\) and is therefore worse than stacking by average which is generally preferred.
Pixel Maximum stacking
This algorithm is mainly used to construct long exposure star-trails images. Pixels of the image are replaced by pixels at the same coordinates if intensity is greater.
Pixel Minimum stacking
This algorithm is mainly used for cropping sequence by removing black borders. Pixels of the image are replaced by pixels at the same coordinates if intensity is lower.
Input normalisation methods
Normalisation will adjust the levels of each image against the reference image. This is particularly useful for mean stacking with rejection, because rejecting pixels if the images show differences of levels is not very useful. They can be caused by light nebulosity, light gradient caused by the moon or city lights, sensor temperature variation and so on.
This tends to improve the signal-to-noise ratio and therefore this is the option used by default with the additive normalisation.
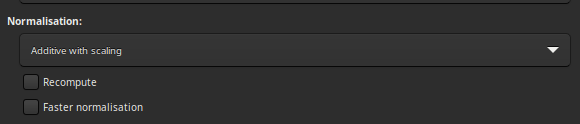
If one of these 5 items is selected, a normalisation process will be applied to all input images before stacking.
Normalisation matches the mean background of all input images, then, the normalisation is processed by multiplication or addition. Keep in mind that both processes generally lead to similar results but multiplicative normalisation is prefered for image which will be used for multiplication or division as flat-field.
Scale matches dispersion by weighting all input images. This tends to improve the signal-to-noise ratio and therefore this is the option used by default with the additive normalisation.
Normalisation |
Operation |
Use case |
||
|---|---|---|---|---|
None |
No normalisation are applied. |
dark/bias frames |
||
Additive |
Mean background values will be aligned through the application of additive operations. |
|||
Multiplicative |
Division will be used to align mean background values. |
flat frames |
||
Additive + Scaling |
In combination with additive background through additive matching, the images will be scaled to achieve dispersion matching. |
light frames |
||
Multiplicative + Scaling |
In combination with background matching through division, the images will be scaled to achieve dispersion matching. |
|||
Note
The bias and dark masters should not be processed with normalisation. However, multiplicative normalisation must be used with flat-field frames.
Keep in mind that both processes generally lead to similar results but multiplicative normalisation is preferred for image which will be used for multiplication or division as flat field.
Since the normalisation calculation step is usually a long one, as it requires
determining all the statistics of the image, the results are stored in the
seq file. This way, if the user wants to do another stacking by changing
the rejection parameters, it will be executed more quickly.
The Recompute option allows to force the recalculation of the
normalisation.
By default, Siril uses IKSS estimators of location and scale to compute normalisation. For long sequences, computing these estimators can be quite intensive. For such cases, you can opt in for faster estimators (based on median and median absolute deviation) with the option Faster normalisation. While less resistant to outliers in each image, they can still give a satisfactory result when compared to no normalisation at all.
Image rejection
It is also possible to reject a certain number of images in order to select only the best ones. This can be very useful for Lucky DSO techniques where the number of images in a sequence is very high. One can choose between % and k-\(\sigma\) to either retain a given percentage of images or to calculate the allowable threshold using k-\(\sigma\) clipping.
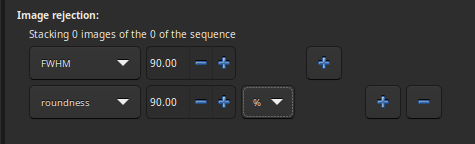
Several critieria are available:
all: all images of the sequence are used in the stack.
selected: only use image that have not been unselected from the sequence.
FWHM: images with best computed FWHM (star-based registration only).
weighted FWHM: this is an improvement of a simple FWHM. It allows to exclude much more spurious images by using the number of stars detected compared to the reference image (star-based registration only).
roundness: images with best star roundness (star-based registration only).
background: images with lowest background values (star-based registration only).
nb stars: images with best number of stars detected (star-based registration only).
quality: images with best quality (planetary DFT or Kombat registrations).
Stacking result
If Output Normalisation is checked, the final image will be normalized in the [0, 1] range if you work in 32-bit format precision, or in [0, 65535] otherwise.
Warning
This option should not be checked for master stacking.
If RGB equalization is checked, the channels in the final image will be equalized (color images only).
The stacking result is saved under the name given in the text field. It is possible to use path parsing to build the filename. A click on the overwrite button allows the new file created to overwrite the old one if it exists. If the latter is not checked but an image with the same name already exists, then no new file is created.
References
Peter J. Huber and E. Ronchetti (2009), Robust Statistics, 2nd Ed., Wiley
Juan Conejero, ImageIntegration, Pixinsight Tutorial
Rosner, B. (1983). Percentage points for a generalized ESD many-outlier procedure. Technometrics, 25(2), 165-172.