Déconvolution
La déconvolution est un outil mathématique permettant de compenser les effets de flou ou de distorsion dans une image. La véritable scène n'est pas ce qui est enregistré par votre capteur - vous enregistrez une estimation de la véritable scène convoluée par une PSF (en termes mathématiques, le "flou PSF" qui représente la distorsion atmosphérique, les propriétés physiques de votre télescope, le flou de mouvement, etc., dégradant votre estimation). La déconvolution peut, dans une certaine mesure, inverser cette dégradation d'image. Cependant, il est important de dire dès le départ que la déconvolution est ce que les mathématiciens appellent un problème mal posé (comme la plupart des problèmes inverses). Mal posé signifie qu'une solution peut ne pas exister, si une solution existe, elle peut ne pas être unique et elle peut ne pas avoir de dépendance continue par rapport aux données. Essentiellement, cela signifie que la déconvolution est, même théoriquement, très difficile et qu'il n'y a aucune garantie que cela fonctionnera.
Tout cela est encore plus difficile lorsque nous ne connaissons pas exactement la PSF que nous essayons de supprimer. En astronomie, nous pouvons théoriquement avoir une idée de la PSF grâce à l'effet de flou sur les sources ponctuelles (étoiles) que nous imagons. Cependant, parfois la véritable PSF n'est pas constante à travers l'image, parfois d'autres facteurs tels que la saturation des étoiles empêchent la PSF de l'étoile d'être une estimation entièrement précise de la PSF, et parfois (par exemple pour l'imagerie lunaire) il n'y a pas d'étoiles.
Siril vise à fournir une approche flexible de la déconvolution. Il existe plusieurs options pour définir ou estimer la PSF, et plusieurs algorithmes de déconvolution à choisir pour l'étape finale de la déconvolution une fois que la PSF est définie.

Exemple de déconvolution sur un champ d'étoiles.
La déconvolution est accessible par le menu Traitement de l'image ou par les commandes Siril.
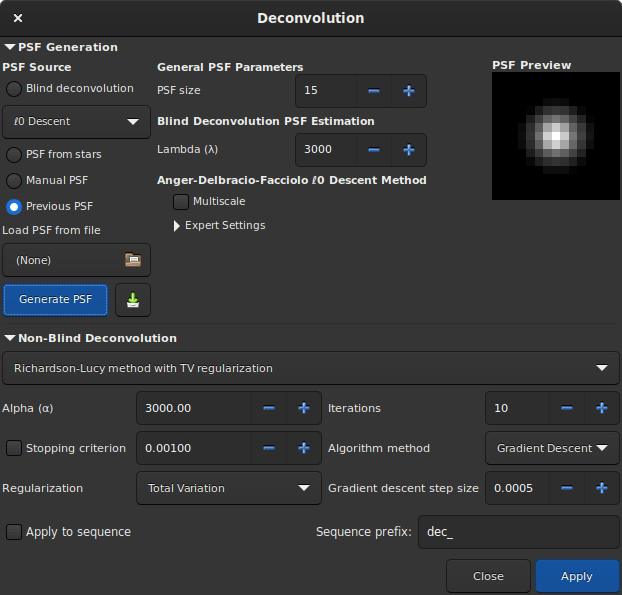
Boite de dialogue de l'outil déconvolution.
Vue d'ensemble de l'utilisation
Pour générer une PSF de déconvolution, sélectionnez la méthode de génération de PSF requise et appuyez sur Générer PSF. Cette opération peut être effectuée séparément de la déconvolution proprement dite afin que l'utilisateur puisse voir l'effet de la modification des paramètres de la PSF.
Siril ne génère que des PSF monochromes car il s'agit du cas d'utilisation le plus courant et cela simplifie l'interface utilisateur. Cependant, trois PSF monochromes peuvent être sauvegardées et composées pour produire une PSF à 3 canaux qui peut être chargée et utilisée pour déconvoluer des images à 3 canaux.
Pour appliquer la déconvolution à une seule image, sélectionnez la méthode de génération de PSF requise et appuyez sur Appliquer. Si une méthode d'estimation de PSF aveugle a été exécutée précédemment, la méthode sera automatiquement définie sur PSF précédente, afin d'éviter de recalculer inutilement la PSF.
Pour appliquer la déconvolution à une séquence, procédez comme ci-dessus mais assurez-vous de cocher l'option Appliquer à la séquence. Vous pouvez également spécifier un préfixe personnalisé à donner à la séquence de sortie : si aucun autre préfixe n'est fourni, le préfixe par défaut (
dec_) sera utilisé.Lors de la déconvolution d'une séquence, la PSF sera calculée uniquement pour la première image. La même PSF sera réutilisée pour toutes les images de la séquence.
Aperçu des méthodes de définition du noyau de flou
Descente \(\boldsymbol{ℓ_0}\) : Il s'agit de la méthode d'estimation de la PSF par défaut, basée sur les travaux d'Anger, Delbracio et Facciolo. Les paramètres n'ont généralement pas besoin d'être ajustés, à l'exception des PSF particulièrement grandes pour lesquelles vous pouvez essayer le modèle d'estimation des PSF à plusieurs échelles. Ce dernier est désactivé par défaut car, au cours du développement, il a été constaté qu'il avait tendance à produire des résultats peu naturels avec les tailles de PSF les plus courantes, petites ou moyennes.
Irrégularités spectrales [Goldstein2012] : Cette méthode d'estimation de la PSF est proposée comme alternative. En général, elle n'est pas aussi performante que la méthode de descente \(ℓ_0\), mais elle peut être utile si vous découvrez une image pour laquelle la méthode par défaut ne donne pas de bons résultats. Pour cette méthode, l'image latente nette ne doit pas contenir de bords tant que le modèle de décroissance spectrale est respecté. D'autre part, la méthode de descente \(ℓ_0\) suppose un modèle similaire (puisque les bords ont la même décroissance spectrale), mais nécessite d'avoir des gradients peu denses et d'être contrastée, donc les bords doivent être en phase, donc théoriquement ce modèle peut fonctionner mieux sur des images sans étoiles et peu contrastées. Ce modèle peut donc théoriquement mieux fonctionner sur les images sans étoile à faible contraste. Il faudra probablement expérimenter pour trouver l'algorithme qui correspond le mieux à vos données.
PSF à partir d'étoiles : Cette méthode modélise une PSF à partir de la PSF moyenne des étoiles sélectionnées. Il est important d'être sélectif dans le choix des étoiles : elles ne doivent pas être saturées, car cela entraînerait une distorsion importante de l'estimation de la PSF, mais elles ne doivent pas non plus être si faibles que les fonctions d'analyse d'étoiles de Siril fournissent des mesures inexactes des étoiles. Les étoiles choisies doivent être raisonnablement brillantes, assez centrales dans l'image et dans une zone de l'image avec un arrière-plan assez constant. Une fois les étoiles sélectionnées, vous pouvez choisir un modèle de profil d'étoile gaussien ou de Moffat et, lors de l'exécution de la déconvolution, la PSF sera synthétisée à partir des paramètres moyens des étoiles sélectionnées. Si aucune étoile n'est sélectionnée, Siril tentera d'auto-détecter les étoiles dont l'amplitude du pic est comprise entre 0,07 et 0,7, avec un profil de Moffat. Cette plage permet d'éviter les étoiles saturées ainsi que celles qui sont trop faibles pour donner une solution précise, et fournit généralement de bons résultats.
PSF manuelle : Cette méthode vous permet de définir une PSF manuellement. Il est possible de définir des modèles de PSF gaussiens, de Moffat ou en disque. Notez que la FWHM est spécifiée en pixels et non en secondes d'arc. Les modèles gaussiens et de Moffat conviennent à la déconvolution des formes d'étoiles résultant de la distorsion atmosphérique ; le modèle de PSF de disque convient à la déconvolution de l'effet d'un léger défaut de mise au point.
Charger une PSF à partir d'un fichier : Cette méthode vous permet de charger une PSF à partir de n'importe quel format d'image supporté par Siril. La PSF fournie doit être carrée (elle sera rejetée si elle n'est pas carrée) et doit être impaire (elle sera recadrée d'un pixel dans chaque direction si elle n'est pas impaire, mais cela donnera une PSF légèrement décentrée et n'est pas optimal par rapport à la fourniture d'une PSF impaire dès le début). Des PSF monochromes ou à trois canaux peuvent être chargées. Si une PSF à 3 canaux est chargée en conjonction avec une image monochrome, les valeurs de luminance uniformément pondérées de la PSF seront utilisées. Si une PSF à 3 canaux est chargée avec une image à 3 canaux, chaque canal de l'image sera déconvolué en utilisant le canal correspondant de la PSF. Si unePSF monochrome est chargée avec une image à 3 canaux, l'image sera convertie dans l'espace couleur LAB et le canal L (Luminance) sera déconvolué en utilisant la PSF monochrome pour des raisons d'efficacité de calcul, et le L déconvolué sera recombiné avec les canaux A et B et reconverti en RVB.
PSF précédente : Cette méthode permet de réutiliser la PSF précédemment estimée. Elle est surtout utile avec les méthodes d'estimation de la PSF en aveugle : si vous êtes satisfait de la PSF estimée mais que vous souhaitez effectuer un certain nombre de tests en utilisant différents paramètres pour l'étape finale de la déconvolution, vous pouvez réutiliser la PSF précédente et économiser du temps de calcul.
Une fois estimées, les PSF peuvent être sauvegardées si on le souhaite. Si Siril est compilé avec le support libtiff, la PSF sera sauvegardée au format TIFF 32 bits, avec le même nom de fichier que l'image courante, mais horodaté et suffixé par
_PSF. Si Siril a été construit sans le support de libtiff, le PSF sera sauvegardé sous la forme d'un fichier FITS. Bien que ce soit le format principal de Siril pour les fichiers d'images astronomiques, le format TIFF est préféré pour les PSF : l'inconvénient d'utiliser le format FITS pour les PSF est une compatibilité réduite avec les éditeurs d'images que vous pourriez souhaiter utiliser pour éditer ou examiner le fichier sauvegardé.
Astuce
Si la génération aveugle d'une PSF de déconvolution peut se faire sur des données linéaires et non linéaires, l'utilisation d'une PSF à partir d'une PSF d'étoile ne peut se faire que sur des images linéaires. Dans le cas contraire, les valeurs de PSF ne seraient pas valides.
Vue d'ensemble de la déconvolution non aveugle
Déconvolution Richardson-Lucy [Lucy1974] : Il s'agit de l'algorithme de déconvolution non aveugle par défaut. Il s'agit d'une méthode itérative, célèbre pour son utilisation dans la correction des distorsions d'image au début de la période d'exploitation du télescope spatial Hubble. Dans Siril, il est régularisé en utilisant soit la méthode de variation totale, qui vise à pénaliser l'algorithme pour l'amplification du bruit, soit la norme de Frobenius de la matrice hessienne locale. Cette régularisation est basée sur les dérivées secondes. En plus de la régularisation, un paramètre d'arrêt précoce est fourni, qui permet d'arrêter l'algorithme dès que son taux de convergence tombe en dessous d'un certain niveau. L'augmentation de la valeur du paramètre d'arrêt précoce permet de réduire les artefacts autour des étoiles et des arêtes (trop) vives. Deux formulations de l'algorithme de Richardson-Lucy sont fournies : la formulation multiplicative et la formulation de descente de gradient. Cette dernière permet un meilleur contrôle, car la taille du pas de descente du gradient peut être modifiée (l'inconvénient est qu'en utilisant des plus petits pas, plus d'itérations sont nécessaires pour atteindre le même niveau de convergence). Le plus grand avantage de la méthode de descente de gradient est qu'elle permet d'utiliser une plus grande régularisation - ce qui peut être problématique dans l'algorithme multiplicatif de Richardson-Lucy car le terme de régularisation apparaît dans le dénominateur et de petites valeurs ici (forte régularisation) peuvent causer de l'instabilité. Siril utilisera la convolution naïve pour les noyaux de petite taille et la convolution basée sur les FFT pour les noyaux de plus grande taille où les FFT fournissent un algorithme plus efficace. (Ceci est automatique et ne nécessite aucune intervention de l'utilisateur.)
Méthode de filtrage de Wiener : Cette méthode est une méthode de déconvolution non itérative. Elle modélise un profil de bruit supposé gaussien, c'est-à-dire un bruit modélisé par un profil constant. La constante alpha est utilisée pour définir la force de régularisation par rapport au niveau de bruit. Comme pour les autres algorithmes, une valeur plus petite pour alpha permet une plus grande régularisation. Cet algorithme peut être bon pour les images lunaires où le régime de bruit est gaussien et non de Poisson, mais il fonctionne généralement mal sur les images de ciel profond où le bruit a toujours tendance à avoir un caractère de Poisson.
Méthode de Split Bregman : Cette méthode est utilisée en interne dans les processus d'estimation de la PSF et est également proposée comme algorithme de déconvolution en phase finale. Il s'agit d'un algorithme couramment utilisé pour résoudre les problèmes d'optimisation convexe. Cet algorithme est également régularisé à l'aide d'une fonction de coût de variation totale. Il n'est pas aussi performant que l'algorithme de Richardson-Lucy pour les paysages étoilés, mais il peut être envisagé pour les images sans étoiles ou les images de la surface lunaire.
Astuce
Le choix de la méthode de déconvolution est très important pour obtenir de bons résultats. En général, pour les images de ciel profond, il est important d'utiliser une méthode de Richardson-Lucy : les méthodes de Split Bregman et de Wiener donnent de mauvais résultats autour des étoiles en raison de la gamme dynamique extrême. Pour les images linéaires, il est généralement préférable d'utiliser les méthodes de Richardson-Lucy à descente de gradient, et si des artefacts apparaissent autour des étoiles brillantes, il faut alors réduire la taille du pas. Cette approche réduit l'impact de chaque itération, ce qui nécessite un plus grand nombre d'itérations, mais cela signifie que vous pouvez obtenir un contrôle plus fin en effectuant la déconvolution jusqu'au point où les artefacts commencent à se former, puis en revenant très légèrement en arrière. Pour les images étirées, les algorithmes multiplicatifs de Richardson-Lucy peuvent être utilisés.
Astuce
Pour les images lunaires et planétaires empilées, les méthodes de Split Bregman ou de Wiener peuvent être plus appropriées. Ces méthodes ne nécessitent généralement pas d'itération comme le fait Richardson-Lucy, et elles peuvent être mieux adaptées aux caractéristiques de bruit des images empilées à rapport signal/bruit élevé. (L'algorithme de Richardson-Lucy est basé sur l'hypothèse d'un bruit de Poisson, ce qui est généralement vrai pour l'imagerie de ciel profond, alors que la méthode de Wiener mise en œuvre ici suppose une distribution de bruit gaussienne qui peut mieux convenir aux images planétaires/lunaires empilées).
Paramètres et Réglages
Paramètres généraux
Taille PSF. La taille de la PSF d'entrée doit être choisie suffisamment grande pour garantir que la PSF est incluse dans le domaine spécifié. Toutefois, si elle est trop grande, les méthodes d'estimation aveugle de la PSF peuvent donner des résultats moins bons et plus longs à calculer.
Lambda (\(\lambda\)). Paramètre de régularisation pour l'estimation de la PSF. Essayez de diminuer cette valeur pour les images bruitées.
Paramètres d'estimation de la PSF de descente de \(\boldsymbol{ℓ_0}\)
Multi-échelle. Ce paramètre active l'estimation de la PSF à plusieurs échelles. Cela peut aider à stabiliser l'estimation de la PSF lorsque l'on spécifie une grande taille de PSF, mais certaines PSF générées avec cette option peuvent donner lieu à des résultats peu naturels et elle est donc désactivée par défaut.
Paramètres experts. Ils ne devraient normalement pas nécessiter de réglage, mais sont mis à la disposition des curieux.
Gamma définit la force de régularisation utilisée lors de l'étape de prédiction de l'image déconvoluée. Pour un gamma donné, l'estimation devient aussi plus bruitée à mesure que le bruit augmente. Si gamma est augmenté, l'estimation est moins affectée par le bruit mais tend à être plus lisse. La valeur par défaut de 20 a été déterminée expérimentalement dans [Anger2019].
Itérations définit le nombre d'itérations utilisées dans la procédure d'estimation de la PSF. Les auteurs de l'algorithme indiquent qu'il n'y a que peu d'avantages à augmenter ce nombre à 3 et qu'il n'y a aucun avantage à l'augmenter au-delà de 3.
Le rapport lambda et le minimum lambda définissent les paramètres permettant d'affiner la prédiction de l'image nette par le biais de valeurs successives du paramètre de régularisation du prédicteur d'image nette à chaque itération de la méthode.
Le facteur d'échelle, le flou de suréchantillonnage et Sous-échantillonner le flou ne sont utilisés que lorsque l'estimation multi-échelle est active. Ils définissent le facteur d'échelle par défaut entre chaque niveau d'échelle et la quantité de flou à utiliser lors de la remise à l'échelle entre chaque échelle.
Seuil du noyau. Les valeurs inférieures à ce niveau dans l'estimation de la PSF sont mises à zéro.
Paramètre de la détermination de la PSF par irrégularité spectrale
Le facteur de compensation contrôle la force d'un filtre utilisé pour éviter une netteté excessive dans la PSF estimée. Pour les images présentant un flou intrinsèque, il convient d'utiliser une valeur proche de l'unité. Pour les images intrinsèquement nettes, des valeurs faibles peuvent entraîner des artefacts et la valeur doit être augmentée jusqu'à un grand nombre, ce qui désactive effectivement le filtre.
Paramètres experts. Ils ne devraient normalement pas nécessiter de réglage, mais sont mis à la disposition des curieux.
Itérations de la boucle interne définit le nombre d'itérations effectuées dans la boucle intérieure de la méthode d'irrégularité spectrale. L'algorithme converge rapidement et il peut être possible de réduire ce nombre à environ 100 sans trop dégrader le résultat.
Échantillons par boucle externe. Ce paramètre contrôle le nombre de phases aléatoires à échantillonner. Étant donné que la récupération de la phase commence par des valeurs aléatoires pour chaque échantillon, il est important de tirer suffisamment d'échantillons pour éviter de converger vers un minimum local. La PSF se stabilise rapidement pour les images à faible bruit, mais si vous cherchez à améliorer les résultats de cette méthode, c'est le premier des paramètres experts à essayer d'ajuster, en particulier avec des images présentant des niveaux de bruit plus élevés.
Itération de la boucle externe. [Anger2018], suggère que 2 itérations peuvent suffire à produire une estimation plausible de la PSF, et qu'il est négligeable d'augmenter ce nombre au-delà de 3.
PSF des étoiles
Cette méthode de génération de PSF n'a pas de paramètres ajustables. Elle génère une PSF basée sur les paramètres moyens des étoiles sélectionnées, en utilisant la commande findstar ou la boîte de dialogue PSF Dynamique. Les paramètres moyens sont affichés dans la boîte de dialogue de déconvolution lorsque cette méthode de génération de PSF est sélectionnée. Il est préférable que l'utilisateur sélectionne activement les étoiles qu'il souhaite utiliser pour cette méthode, afin d'obtenir la PSF la plus précise. Idéalement, une dizaine d'étoiles assez brillantes mais non saturées devraient être sélectionnées dans la région centrale de l'image (pour exclure les étoiles qui peuvent souffrir de coma ou d'autres aberrations). Cependant, si l'utilisateur n'a sélectionné aucune étoile, Siril tentera de détecter automatiquement les étoiles appropriées en exécutant sa routine de détection avec des filtres réglés pour ne conserver que les étoiles dont les amplitudes de crête sont comprises entre 0,07 et 0,7. Cette plage permet d'éviter les étoiles saturées et celles qui sont trop faibles pour donner une solution précise. Cette méthode fonctionne bien dans la plupart des cas, mais peut encore être affectée par des aberrations hors centre.
Si vous cochez la case PSF symétrique, la PSF générée sera circulaire. Cela correspondra à la moyenne des FWHM et beta des étoiles sélectionnées mais ne correspondra à aucune élongation.
PSF manuel
Cette méthode de génération de PSF permet de spécifier une PSF paramétrique personnalisée.
Profil permet de choisir le profil de la PSF. Les profils Gaussien, Moffat, disque et dique d'Airy sont supportés.
Les PSF gaussiennes et de Moffat sont utilisées pour faire correspondre les paramètres des étoiles mesurés à partir de l'image. Elles devraient fournir une bonne estimation de la fonction de flou totale appliquée à l'image, car les étoiles sont des sources ponctuelles.

Un exemple d'une PSF avec un profil Moffat avec fwhm=5", Angle=45°, Ratio=1.20, \(\beta=4.5\) et une taille de PSF de 15.
Les PSF disque sont utilisés pour déconvoluer les images qui ne sont pas au point.

Un exemple de profil Disque avec fwhm=5" et une taille de PSF de 15.
La PSF de disque d'Airy est utilisée pour déconvoluer la diffraction qui est la conséquence physique de la diffraction par l'ouverture de votre télescope.

Exemple d'une PSF d'un disque d'Airy avec Diamètre = 250mm, Longueur focal = 4500mm, Longueur d'onde = 525nm, Taille Pixel = 2.9µm, Obstruction Centrale = 40% et avec une taille de PSF de 41.
FWHM spécifie la largeur à mi-maximum du profil choisi (pour les PSFs de disque, il spécifie simplement le rayon).
Beta (\(\beta\)) spécifie le paramètre beta utilisé pour le profil de PSF Moffat. Il est ignoré par les autres profils de PSF.
Pour les PFS du disque d'Airy, un certain nombre de paramètres de votre télescope et de votre capteur sont nécessaires :
Ouverture
Longueur focale
Taille de pixel du capteur
Longueur d'onde centrale de l'image. Siril essaiera d'extraire ces données des métadonnées de l'image lorsqu'elles sont disponibles, mais si certains paramètres sont manquants ou semblent déraisonnables, Siril les mettra en évidence et imprimera un avertissement dans le log vous recommandant de les vérifier. Le rapport de l'obstruction centrale est également nécessaire pour générer un disque d'Airy précis. Il est exprimé en pourcentage, c'est-à-dire que la surface totale de l'obstruction centrale est divisée par la surface totale de l'ouverture x 100. Pour les réfracteurs (avec des lentilles), ce pourcentage est nul ; pour les autres télescopes, il varie : il peut être d'environ 20 % pour un réflecteur newtonien ou de 40 à 50 % pour certains télescopes Dall-Kirkham corrigés. Vous devrez mesurer votre instrument ou consulter les spécifications du fabricant.
Déconvolution de Richardson-Lucy
Les paramètres utilisés pour configurer la déconvolution de Richardson-Lucy dans Siril sont les suivants :
alpha définit l'intensité de la régularisation. Une valeur plus petite d'alpha donne une régularisation plus forte et un résultat plus lisse ; une valeur plus grande réduit la force de régularisation et préserve plus de détails de l'image, mais peut entraîner l'amplification du bruit.
Itérations spécifie le nombre maximum d'itérations à utiliser. En l'absence de bruit, un grand nombre d'itérations fera converger l'estimation de la déconvolution plus près de l'image réelle, mais un nombre excessif d'itérations amplifiera également le bruit et provoquera des artefacts en annaux autour des étoiles. La valeur par défaut est 1 itération : un nombre plus élevé peut être défini pour calculer plusieurs itérations automatiquement, ou vous pouvez continuer à appuyer sur Appliquer pour appliquer une itération à la fois jusqu'à ce que vous soyez satisfait du résultat. (Ou aller plus loin, décider que vous n'êtes plus satisfait et utiliser Annuler.)
Critère d'arrêt définit un critère de convergence basé sur les différences d'estimation successives. L'algorithme s'arrête lorsque la convergence se situe dans la limite spécifiée. Il s'agit d'un paramètre important - si vous obtenez des anneaux autour des étoiles dans votre image finale, essayez d'augmenter la valeur du critère d'arrêt. Ce paramètre peut être complètement désactivé à l'aide du bouton à cocher.
Méthode d'algorithme spécifie s'il faut utiliser l'implémentation multiplicative ou l'implémentation par descente de gradient.
Taille du pas spécifie la taille du pas à utiliser pour l'implémentation de la descente de gradient. Ce paramètre ne doit pas être trop grand, sinon l'algorithme ne convergera pas. Ce paramètre n'a aucun effet si l'implémentation multiplicative est sélectionnée.
Astuce
Pour les images linéaires, l'utilisation des méthodes de descente de gradient permet d'obtenir le contrôle nécessaire pour éviter la formation d'anneaux autour des étoiles. Cependant, pour la déconvolution d'images étirées, cette méthode peut être inutilement lente. L'utilisation de méthodes multiplicatives permet donc souvent de gagner du temps sans compromettre la qualité de l'image.
Déconvolution de Split Bregman
Les paramètres utilisés pour configurer la déconvolution de Split Bregman dans Siril sont les suivants :
alpha définit l'intensité de la régularisation. Une valeur plus petite d'alpha donne une régularisation plus forte et un résultat plus lisse ; une valeur plus grande réduit la force de régularisation et préserve plus de détails de l'image, mais peut entraîner l'amplification du bruit.
Itérations spécifie le nombre maximum d'itérations à utiliser. La méthode Split Bregman ne nécessite pas d'itérations multiples dans la forme implémentée ici, mais peut être itérée si on le souhaite. Cela ne fait généralement qu'une petite différence et la valeur par défaut est donc 1.
Déconvolution de Wiener
La déconvolution de Wiener dans Siril ne nécessite qu'un seul paramètre :
alpha définit l'intensité de la régularisation. Une valeur plus petite d'alpha donne une régularisation plus forte et un résultat plus lisse ; une valeur plus grande réduit la force de régularisation et préserve plus de détails de l'image, mais peut entraîner l'amplification du bruit.
Paramètres de performance de la FFTW
Les algorithmes d'estimation et de déconvolution de la PSF font un usage intensif des transformées de Fourier rapides à l'aide de la bibliothèque FFTW. Ceci offre un certain nombre d'options de réglage, qui peuvent être ajustées dans l'onglet performance du dialogue principal Siril préférences.
Note sur l'ordre des lignes de l'image
Les différents types d'images traitées par Siril peuvent avoir leurs données de pixels arrangées dans des ordres différents. Les fichiers vidéo SER stockent toujours les données de haut en bas, tandis que les fichiers FITS peuvent stocker les données de bas en haut ou de haut en bas. L'ordre ascendant est la recommandation initiale, mais de plus en plus de fichiers FITS proviennent de caméras CMOS qui ont tendance à suivre un ordre descendant des pixels.
Lorsqu'une image est déconvoluée avec une PSF créée à partir de la même image (ou ouverte), cela ne pose aucun problème. Cependant, des problèmes peuvent survenir si une PSF est générée à partir d'une image avec un ordre des lignes et utilisée pour déconvoluer une image ou une séquence avec l'ordre des lignes opposé. Il s'agit d'un cas d'utilisation particulier, mais son traitement systématique donne lieu à un comportement qui, à première vue, peut être surprenant : il est donc expliqué ci-dessous.
Siril traite le problème en suivant l'ordre des lignes de l'image avec laquelle le PSF a été créé. Les PSF sont toujours sauvegardés en utilisant un ordre de rangée ascendant (en les retournant automatiquement s'ils ont été créés avec une image descendante), et lorsqu'ils sont chargés, l'ordre de rangée correspond à l'ordre de rangée de l'image actuellement ouverte. Si une image dont l'ordre des lignes est opposé est ouverte, l'ordre des lignes de la PSF sera modifié pour correspondre. Cela signifie que si, par exemple, vous prenez des images FITS ascendantes, utilisez l'une d'entre elles pour générer une PSF, puis les convertissez en une séquence SER descendante, la PSF sera convertie dans l'orientation correcte pour correspondre à la séquence SER. Si une PSF est en cours de prévisualisation au moment où une image avec l'ordre des lignes opposé est ouverte, la prévisualisation ne sera pas mise à jour immédiatement : le changement d'ordre des lignes sera détecté automatiquement et la PSF sera inversée au moment où elle sera appliquée à l'image.
Galerie
Cette section présente quelques exemples de cas où la déconvolution a mal tourné, ainsi que des explications sur les raisons de ces erreurs.
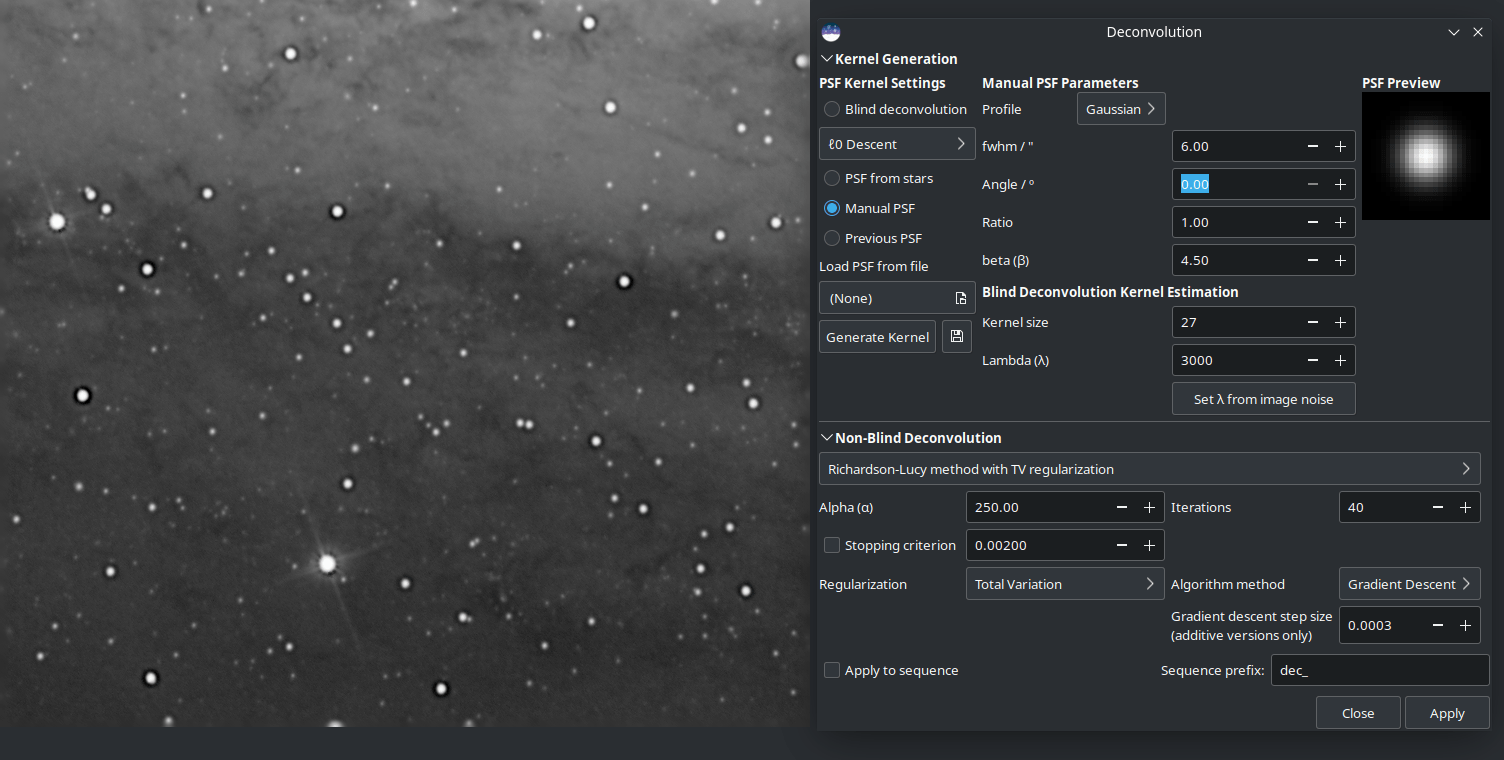
La PSF spécifiée manuellement était trop grande, ce qui se traduisait par de grands anneaux sombres autour des étoiles.
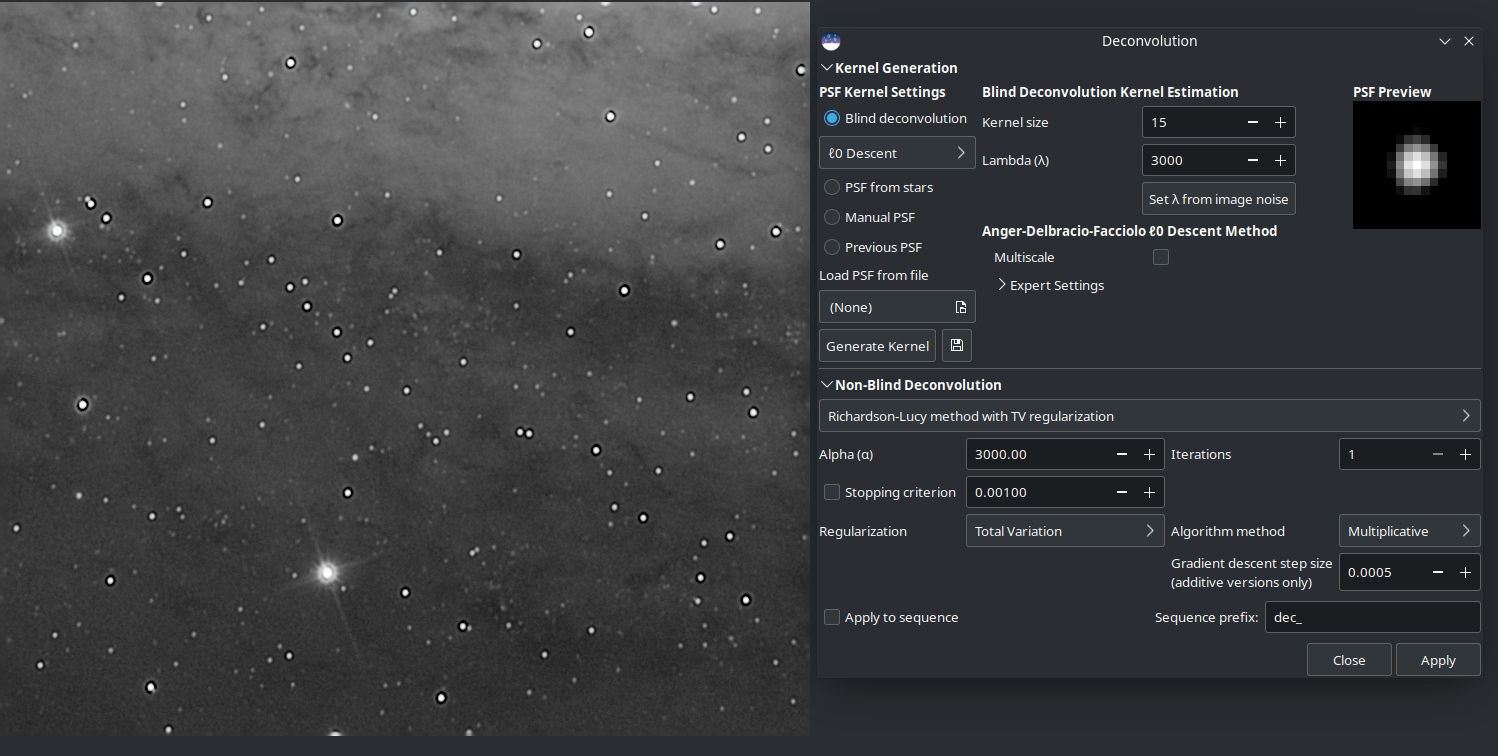
Trop d'itérations ont été appliquées. (Je les ai appliquées une par une pour exagérer le résultat, c'est pourquoi le paramètre itérations indique toujours 1.)

Gros plan montrant l'effet d'une tentative d'application d'une régularisation trop importante (alpha = 30) à l'aide de la version multiplicative de Richardson-Lucy. Pour une forte régularisation et/ou un meilleur contrôle de chaque itération, la formule de descente de gradient est recommandée.
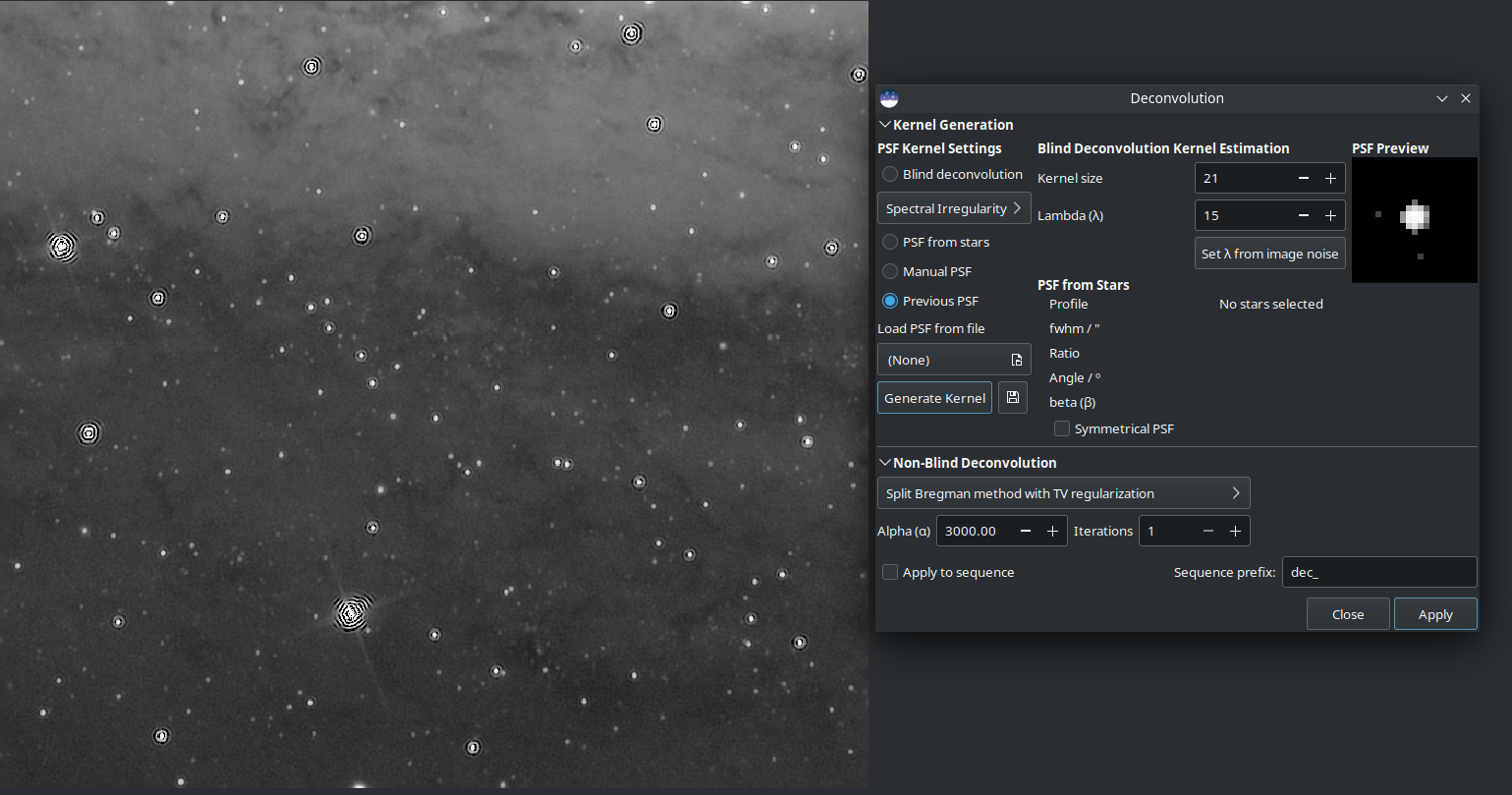
Exemple typique de tentative de déconvolution d'un champ d'étoiles d'une image non étirée à l'aide de la méthode de Split Bregman (dans ce cas) ou de la déconvolution par filtre de Wiener. Ces méthodes sont plus adaptées aux images planétaires, lunaires ou solaires ; pour les paysages stellaires, la méthode Richardson-Lucy est toujours recommandée.
Déconvolution : Conseils d'utilisation
Vous êtes arrivé ici en cliquant sur le bouton "Conseils" de l'outil de déconvolution dans Siril. Ne vous inquiétez pas : la déconvolution est une technique délicate. Même en théorie, elle est vraiment difficile : il n'y a aucune garantie que les mathématiques convergent toujours vers une solution unique qui améliore votre image. Cela dit, voici quelques conseils pour vous aider à tirer le meilleur parti des algorithmes de déconvolution de Siril.
Quelle PSF utiliser ?
L'utilisation d'une PSF précise est fondamentale pour obtenir de bons résultats avec la déconvolution. Les deux façons les plus simples de générer une PSF sont d'utiliser une estimation aveugle de la PSF, ou de modéliser votre PSF sur les étoiles de votre image.
PSF des étoiles
Siril peut détecter et modéliser les étoiles dans votre image. Voir la page d'aide de Dynamic PSF pour plus de détails. Pour obtenir un bon modèle pour votre PSF, essayez de sélectionner le profil d'étoile de Moffat dans PSF Dynamique. Les étoiles sont des sources ponctuelles, donc la fonction d'étalement d'une étoile moyenne est un bon modèle pour les effets de flou que nous essayons d'éliminer par déconvolution.
Astuce
Une fois les étoiles détectées, triez-les par amplitude de pic (paramètre "A"). Sélectionnez et supprimez celles dont l'amplitude est supérieure à 0,7 ou inférieure à 0,1, et si votre image contient des galaxies de fond, vérifiez qu'il ne reste pas de faux positifs. Les étoiles dans cette gamme de luminosité ne sont pas saturées et pas trop faibles pour donner un modèle PSF précis.
Astuce
Si la génération aveugle d'une PSF de déconvolution peut se faire sur des données linéaires et non linéaires, l'utilisation d'une PSF à partir d'une PSF d'étoile ne peut se faire que sur des images linéaires. Dans le cas contraire, les valeurs de PSF ne seraient pas valides.
Estimation de la PSF en aveugle
Ces méthodes peuvent estimer automatiquement une PSF sur la base de l'image elle-même. Si vous n'avez pas de meilleures connaissances préalables de la PSF, comme des étoiles dans l'image (par exemple, une imagerie lunaire qui ne contient pas d'étoiles), cela peut être votre meilleure option. Dans la plupart des cas, il est recommandé d'utiliser la méthode par défaut \(\boldsymbol{ℓ_0}\) : elle est plus rapide et donne généralement de meilleurs résultats.
Astuce
Quelle que soit la façon dont vous générez votre PSF, vérifiez l'aperçu pour vous assurer qu'elle ne semble pas tronquée. Si c'est le cas, augmentez la taille de la PSF jusqu'à ce qu'aucune partie significative de la PSF ne soit coupée.
Autres méthodes de génération de PSF
D'autres méthodes de génération de PSF méritent d'être mentionnées : le profil de disque manuel et le disque d'Airy. Le profil de disque peut être utilisé pour améliorer les images dont la mise au point est légèrement décalée. Essayez de faire correspondre la taille du disque à la taille du flou hors foyer. Le disque d'Airy peut être utilisé pour corriger le léger flou causé par la diffraction du tube du télescope lui-même.
Astuce
Si vous avez un seeing exceptionnel (peu ou pas de flou atmosphérique), la déconvolution de l'image à l'aide d'un disque d'Airy peut suffire.
La déconvolution de l'image
Une fois que vous avez généré une PSF dont vous êtes satisfait, vous êtes prêt à faire une déconvolution de votre image. Il est important d'utiliser les bons paramètres pour obtenir de bons résultats.
Astuce
La déconvolution est assez lente pour les grandes images. Pour trouver plus rapidement les meilleurs paramètres, sauvegardez votre travail à ce stade et recadrez une petite partie représentative de l'image. Faite une déconvolution avec différents paramètres, en utilisant le bouton Annuler jusqu'à ce que vous soyez satisfait. Puis annulez une fois de plus pour revenir à votre image non recadrée et appliquez les paramètres à l'ensemble de l'image.
Images avec des étoiles
Les images contenant des étoiles, en particulier les données linéaires (non étirées), doivent toujours être déconvoluées à l'aide des méthodes de Richardson-Lucy. Ignorez Split Bregman et Wiener : ces algorithmes sont adaptés aux images d'objets du système solaire.
Les images du ciel profond posent deux défis à la déconvolution : l'anneau autour des étoiles brillantes et l'amplification du bruit de fond.
Pour traiter les anneaux autour des étoiles, essayez d'utiliser la méthode de descente de gradient et augmentez progressivement le nombre d'itérations jusqu'à ce que vous commenciez à voir des signes d'anneaux sombres se former autour des étoiles, puis réduisez légèrement les itérations.
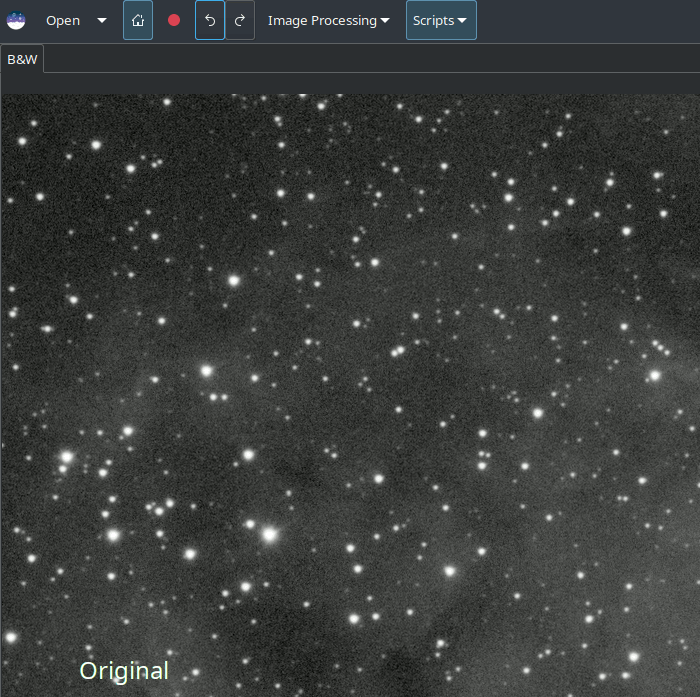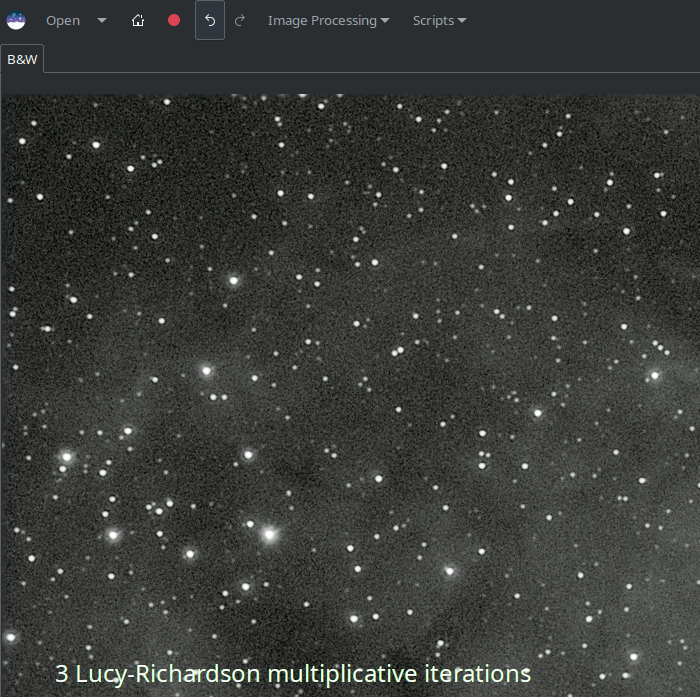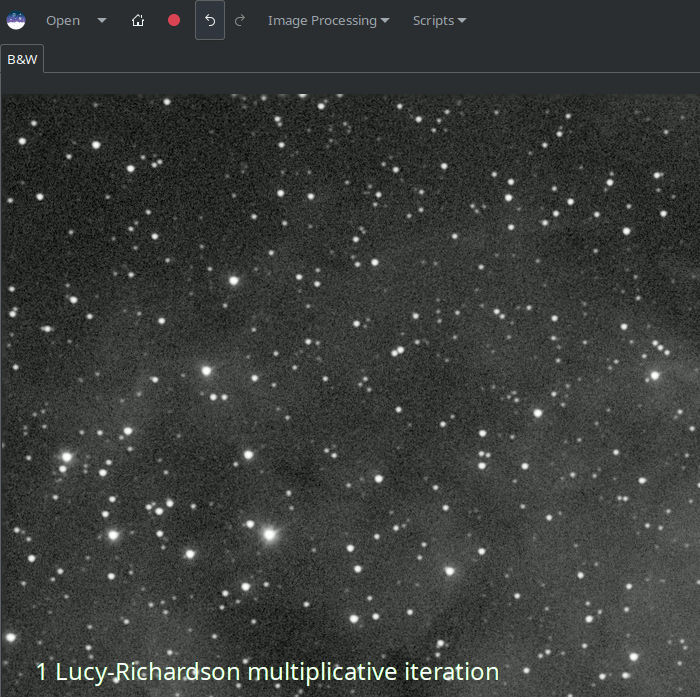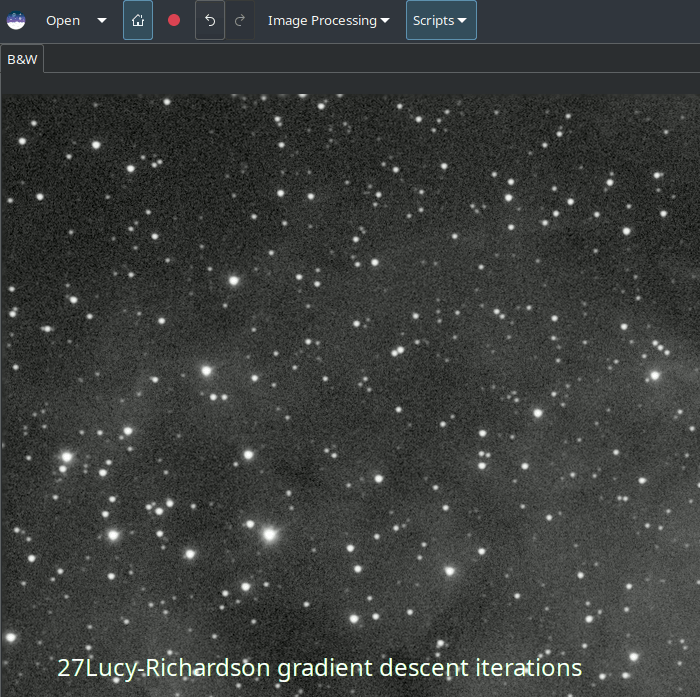
L'animation ci-dessus montre l'effet de la réduction du nombre d'itérations de la formulation multiplicative de Richardson-Lucy : elle démontre également le contrôle plus fin qui peut être obtenu en utilisant la méthode de descente de gradient, au prix d'un plus grand nombre d'itérations.
Pour traiter l'amplification du bruit de fond, vous pouvez essayer d'appliquer une petite réduction du bruit avant la déconvolution. Dans la boîte de dialogue Réduction de bruit choisissez l'algorithme de débruitage secondaire Anscombe VST et laissez la modulation assez basse, essayez autour de 50-60%. Vous voulez juste atténuer le bruit pour vous permettre de pousser le nombre d'itérations un peu plus loin, sans générer une image complètement lisse.
Images Lunaires
En général, vous pouvez souhaiter augmenter la netteté d'une image lunaire après l'avoir empilée. Les images lunaires empilées peuvent être très bien affinées en utilisant les méthodes Split Bregman ou Wiener. Je choisis habituellement la méthode Split Bregman. Essayez de laisser la valeur de \(\boldsymbol{\alpha}\) par défaut, et faire la déconvolution de l'image en utilisant une PSF \(\boldsymbol{ℓ_0}\) estimée en aveugle. Un exemple de ceci est montré ci-dessous en utilisant une image lunaire fraîchement empilée (c'est-à-dire qu'aucun traitement par ondelettes n'a été effectué). Malgré les limitations du format d'animation GIF, l'accentuation est clairement visible ; il est également clair que les résultats de Split Bregman et Wiener sont très similaires.

Images planétaires empilées
Un flux de travail planétaire typique implique l'empilement de la vidéo SER planétaire dans un outil spécialisé tel que Autostakkert! ou Astrosurface, puis l'accentuation de l'image résultante à l'aide d'ondelettes et de déconvolution. Une combinaison de l'outil Siril A trous Wavelets et de l'outil Deconvolution donne d'excellents résultats, comme illustré ici. Cette image de Jupiter a été initialement rendue plus nette à l'aide d'ondelettes, le premier contrôle de couche étant réglé sur 75, le second sur 10 et les autres sur la valeur par défaut. Une PSF couleur a ensuite été construite à partir de 3 disques d'Airy calculés pour le télescope et le capteur utilisés (un Newtonian 6" avec une lentille de Barlow 3x et un capteur ASI462MC avec des pixels de 2,9 microns) et composée à l'aide de l'outil de composition RVB. Ceci a été utilisé pour faire une déconvolution de l'image avec 6 itérations de Richardson-Lucy (ici j'ai utilisé la version multiplicative). A chaque étape, l'image devient plus nette.

Empilement brute, toujours floue.

Traitement avec décomposition en ondelettes de Siril, force de la couche d'ondelettes 1, 75, force de la couche d'ondelettes 2, 10.

Traitée avec les ondelettes de Siril comme ci-dessus, puis avec 6 itérations de déconvolution multiplicative de Richardson-Lucy.
Les séquences planétaires non empilées
Astuce
Attention : cette méthode est extrêmement lente car elle nécessite le traitement individuel de 30 000 images (ou plus) dans une séquence planétaire !
Certains utilisateurs ont suggéré d'atténuer la diffraction du télescope en faisant une déconvolution de la séquence à l'aide d'une PSF de disque d'Airy. Pour ce faire, avec une caméra planétaire couleur typique, la séquence doit être dématricée à la volée. Vous pouvez aller plus loin si vous le souhaitez en générant trois disques d'Airy séparés pour les longueurs d'onde rouge, verte et bleue (typiquement 600nnm, 530nm et 450nm respectivement). Siril ne peut pas générer directement un PSF couleur (l'interface utilisateur de la déconvolution est suffisamment complexe !) mais si vous enregistrez séparément chacun des disques d'Airy rouge, vert et bleu, vous pouvez les combiner en une PSF couleur en utilisant l'outil de composition RVB. Sauvegardez-le, et si une couleur ou une séquence est chargée, la PSF se chargera en couleur et procédera à la déconvolution de chaque canal de couleur en utilisant la PSF appropriée.

Empilés et netteté renforcée sans déconvolution individuelle des images.

Pile brute : les meilleurs 30% de 91k images déconvoluées individuellement en utilisant Siril.

Résultat de l'accentuation de la pile ou une déconvolution a été appliquée sur chaque image individuellement.
Dans l'image ci-dessus, une légère amélioration de la forme du bord est évidente dans la version qui a subit une déconvolution image par image avec une PSF de disque d'Airy en utilisant la méthode Richardson-Lucy de Siril avant l'empilement, mais il faut faire attention pour éviter la perte de détails. Ce processus est très lent : ma machine de développement a mis 4,5 heures pour effectuer la déconvolution de chacune des 91 000 images de cette séquence, et l'amélioration peut être mineure, voire nulle.
Commandes
Ligne de commande Siril
makepsf clear
makepsf load filename
makepsf save [filename]
makepsf blind [-l0] [-si] [-multiscale] [-lambda=] [-comp=] [-ks=] [-savepsf=]
makepsf stars [-sym] [-ks=] [-savepsf=]
makepsf manual { -gaussian | -moffat | -disc | -airy } [-fwhm=] [-angle=] [-ratio=] [-beta=] [-dia=] [-fl=] [-wl=] [-pixelsize=] [-obstruct=] [-ks=] [-savepsf=]
Ligne de commande Siril
rl [-loadpsf=] [-alpha=] [-iters=] [-stop=] [-gdstep=] [-tv] [-fh] [-mul]
Ligne de commande Siril
sb [-loadpsf=] [-alpha=] [-iters=]
Ligne de commande Siril
wiener [-loadpsf=] [-alpha=]
Références
Anger, J., Facciolo, G., & Delbracio, M. (2018). Estimating an image's blur kernel using natural image statistics, and deblurring it: an analysis of the Goldstein-Fattal method. Image Processing On Line, 8, 282-304. https://doi.org/10.5201/ipol.2018.211
Anger, J., Facciolo, G., & Delbracio, M. (2019). Blind image deblurring using the l0 gradient prior. Image processing on line, 9, 124-142. https://doi.org/10.5201/ipol.2019.243
Goldstein, A., & Fattal, R. (2012, October). Blur-kernel estimation from spectral irregularities. In European Conference on Computer Vision (pp. 622-635). Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-33715-4_45
Lucy, L. B. (1974). An iterative technique for the rectification of observed distributions. The astronomical journal, 79, 745. https://doi.org/10.1086/111605.